欧拉恒等式_欧拉恒等式推导全过程

欧拉恒等式_欧拉恒等式推导全过程

       很高兴能够参与这个欧拉恒等式问题集合的解答工作。我将根据自己的知识和经验，为每个问题提供准确而有用的回答，并尽量满足大家的需求。

1.欧拉公式\欧拉方程是什么?

2.欧拉恒等式的介绍

3.euler公式是什么？

4.欧拉公式e^ix=cosx+isinx是什么意思？

5.欧拉公式e^ix=cosx+isinx是怎么推出来的

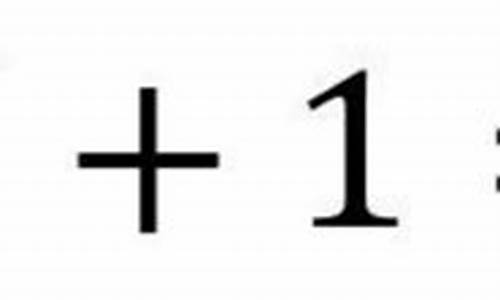
欧拉公式\欧拉方程是什么?

       欧拉公式（英语：Euler's formula，又称尤拉公式）是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名。欧拉公式提出，对任意实数?{\displaystyle x}，都存在。

       欧拉方程，即运动微分方程，属于无粘性流体动力学中最重要的基本方程，是指对无粘性流体微团应用牛顿第二定律得到的运动微分方程。欧拉方程应用十分广泛。1755年，瑞士数学家L.欧拉在《流体运动的一般原理》一书中首先提出这个方程。

扩展资料：

       在物理学上，欧拉方程统治刚体的转动。我们可以选取相对于惯量的主轴坐标为体坐标轴系。这使得计算得以简化，因为我们如今可以将角动量的变化分成分别描述的大小变化和方向变化的部分，并进一步将惯量对角化。

       在流体动力学中，欧拉方程是一组支配无粘性流体运动的方程，以莱昂哈德·欧拉命名。方程组各方程分别代表质量守恒（连续性）、动量守恒及能量守恒，对应零粘性及无热传导项的纳维－斯托克斯方程。历史上，只有连续性及动量方程是由欧拉所推导的。然而，流体动力学的文献常把全组方程——包括能量方程——称为“欧拉方程”。

       百度百科-欧拉方程

欧拉恒等式的介绍

       ∝

        Σ 1/n? = π?/6

       n=1

       这个美妙的数学恒等式，是欧拉用贝努利数的性质推出来的；

       还有世界上最美的公式：

       e^πi+1=0（欧拉公式）

       包含了世界上最美的5个数：e、π、i、1、0

       还有欧拉幻方：

       01 48 31 50 33 16 63 18

       30 51 46 03 62 19 14 35

       47 02 49 32 15 34 17 64

       52 29 04 45 20 61 36 13

       05 44 25 56 09 40 21 60

       28 53 08 41 24 57 12 37

       43 06 55 26 39 10 59 22

       54 27 42 07 58 23 38 11

       还有，他证明了哥尼斯堡七桥问题无解，促进了拓扑学的发展；

       对于任意多面体，V+E-F=2

       其中V是顶点个数，E是面数，F是棱数；

       欧拉是工作到生命最后一刻的数学家，他还有其它许多的数学成就，我还不是很清楚……

euler公式是什么？

       欧拉恒等式也叫做欧拉公式，它是数学里最令人着迷的一个公式，它将数学里最重要的几个常数联系到了一起：两个超越数：自然对数的底e，圆周率π，两个单位：虚数单位i和自然数的单位1，以及数学里常见的0。数学家们评价它是“上帝创造的公式”，我们只能看它而不能理解它。

欧拉公式e^ix=cosx+isinx是什么意思？

       euler公式是欧拉公式，英文全称为Euler's formula。

       欧拉公式是欧哈德·欧拉在十八世纪创造的，是数学界最著名、最美丽的公式之一。之所以如此，是因为它涉及到各种显然非常不同的元素，比如无理数e、虚数和三角函数。R+ V- E= 2就是欧拉公式。

       作用：

       欧拉公式容易理解的有两个作用，一个是用于多面体的，而另外—个是用于级数展开的。欧拉公式数学中起到至关作用的数字被它联系了起来，两个超越数,自然对数的底e和圆周率π两个单位，虚数单位和自然数的单位1以及人类数学史上最伟大的发现0。因此在数学家的眼中，欧拉公式应是上帝的公式。

       第一个证明欧拉公式的人是20岁的柯西，他通过多面体设想的方法肯定了欧拉公式存在的意义。欧拉公式的种变换，欧拉恒等式它被称作是数学中最美妙的一个公式。

欧拉公式e^ix=cosx+isinx是怎么推出来的

       欧拉公式e^(ix)=cosx+isinx只是一个定义，没有推导，你可以认为f（ix）=cosx+isinx；而这个f（ix）很巧妙，和我们已知的e^x性质很像，（比如f（ix）*e^x=f（ix+x））因而写作e^(ix），但实际上并不是传统的e^x，只是一种写法。

       推导过程：

       因为cosx+isinx=e^ix

       cosx-isinx=e^-ix

       两式相加，得：2cosx=e^ix+e^-ix，把2除过去就可以得到cosx=(e^ix+e^-ix)/2。

       两式相减，得：2isinx=e^ix-e^-ix，把2i除过去就可以得到sinx=(e^ix-e^-ix)/2i。

       含义

       恒等式也叫做欧拉公式，它是数学里最令人着迷的一个公式，它将数学里最重要的几个数字联系到了一起：两个超越数：自然对数的底e，圆周率π；两个单位：虚数单位i和自然数的单位1；以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”。

       将函数y=e^x、y=sinx、y=cosx用幂级数展开,有

        e^x=exp(x)＝1＋x/1！＋x^2/2！＋x^3/3！＋x^4/4！＋…＋x^n/n！＋… <1>

        sinx=x-x^3/3!+x^5/5!-x^7/7!+……+(-1)^(k-1)*x^(2k-1)/(2k-1)!+…… <2>

        cosx=1-x^2/2!+x^4/4!-x^6/6!+……+(-1)^k*x^(2k)/(2k)!+…… <3>

       将<1>式中的x换为ix,得到<4>式；

       将i*<2>+<3>式得到<5>式。比较<4><5>两式，知<4>与<5>恒等。

       于是我们导出了e^ix=cosx+isinx，

        将公式里的x换成-x，得到：

       e^-ix=cosx-isinx，然后采用两式相加减的方法得到：

       sinx=(e^ix-e^-ix)/(2i)，cosx=(e^ix+e^-ix)/2.

       tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]

       此时三角函数定义域已推广至整个复数集。

       P.S.

       幂级数

       c0+c1x+c2x2+...+cnxn+...=∑cnxn (n=0..∞)

       c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=∑cn(x-a)n (n=0..∞)

       它们的各项都是正整数幂的幂函数, 其中c0,c1,c2,...cn...及a都是常数, 这种级数称为幂级数.

       泰勒展开式(幂级数展开法):

       f(x)=f(a)+f'(a)/1!*(x-a)+f''(a)/2!*(x-a)2+...f(n)(a)/n!*(x-a)n+...

       实用幂级数：

       ex = 1+x+x2/2!+x3/3!+...+xn/n!+...

       ln(1+x)= x-x2/3+x3/3-...(-1)k-1*xk/k+... (|x|<1)

       sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)

       cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)

       arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)

       arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)

       arctan x = x - x^3/3 + x^5/5 - ... (x≤1)

       sinh x = x+x3/3!+x5/5!+...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)

       cosh x = 1+x2/2!+x4/4!+...(-1)k*x2k/(2k)!+... (-∞<x<∞)

       arcsinh x = x - 1/2*x3/3 + 1*3/(2*4)*x5/5 - ... (|x|<1)

       arctanh x = x + x^3/3 + x^5/5 + ... (|x|<1)

       好了，今天关于“欧拉恒等式”的话题就讲到这里了。希望大家能够通过我的讲解对“欧拉恒等式”有更全面、深入的了解，并且能够在今后的学习中更好地运用所学知识。